Definicion.
Ecuaciones lineales con más de dos variables.
Para sistemas de ecuaciones lineales con más de dos variables, podemos usar el método de eliminación por sustitución o el método de eliminación por suma o resta (por adición o sustracción).
El método de eliminación por suma o resta es la técnica más breve y fácil de hallar soluciones. Además, lleva la técnica de matrices que se estudia en esta sección.
Cualquier sistema de ecuaciones lineales con tres variables tiene una solución única, un número infinito de soluciones o no tiene solución.
Método de eliminación para resolver un sistema de ecuaciones lineales.
El problema consiste en encontrar los valores desconocidos de las variables x1, x2 y x3 que satisfacen las tres ecuaciones.
El problema de los sistemas lineales de ecuaciones es uno de los más antiguos de la matemática y tiene una infinidad de aplicaciones, como en procesamiento digital de señales, estimación, predicción y más generalmente en programación lineal así como en la aproximación de problemas no lineales de análisis numérico.
Clasificacion.
Sistema general
La forma genérica de un sistema de ecuaciones y
ecuaciones y  incógnitas es la siguiente:
incógnitas es la siguiente:donde
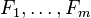 son funciones de las incógnitas. La solución, perteneciente al espacio euclídeo
son funciones de las incógnitas. La solución, perteneciente al espacio euclídeo  , será tal que el resultado de evaluar cualquier expresión
, será tal que el resultado de evaluar cualquier expresión  con los valores de dicha solución, verifique la ecuación.
con los valores de dicha solución, verifique la ecuación.Representación gráfica.
Los sistemas de 2 o 3 incógnitas admiten representaciones gráficas cuando las funciones en () son continuas a tramos. En cada ecuación se representa como una curva o una superficie curva. La existencia de soluciones en ese caso puede deducirse a partir de la existencia de intersecciones comunes a dichas curvas o superficies curvas.
en () son continuas a tramos. En cada ecuación se representa como una curva o una superficie curva. La existencia de soluciones en ese caso puede deducirse a partir de la existencia de intersecciones comunes a dichas curvas o superficies curvas.Clasificación de los sistemas.
Un sistema de ecuaciones sobre puede clasificarse de acuerdo con el número de soluciones en:
puede clasificarse de acuerdo con el número de soluciones en:- Sistema incompatible cuando no admite ninguna solución.
- Sistema compatible cuando admite alguna solución que a su vez pueden dividirse en:
- Sistemas compatibles indeterminados cuando existe un número infinito de soluciones que forman una variedad continua.
- Sistemas compatibles determinados cuando admiten un conjunto finito de soluciones, o un conjunto infinito de soluciones aisladas con a lo sumo un número finito de puntos de acumulación.
Sistema lineal.
Un sistema como el anterior en que las anteriores ecuaciones son funciones afines. A diferencia del caso general, la solución de los sistemas de ecuaciones lineales son fáciles de encontrar cuando los coeficientes de las ecuaciones son números reales o complejos. También existen medios generales cuando los coeficientes pertenecen a un anillo, aunque la búsqueda de las soluciones en ese caso puede ser un poco más complicada.Una característica importante de los sistemas lineales de ecuaciones es que admiten la llamada forma matricial. Esa forma permite representar el sistema usando tres matrices, de la siguiente forma:
La primera es la matriz de coeficientes, donde el término
 representa al coeficiente que acompaña a la j-ésima incógnita de la ecuación i-ésima. La segunda es la matriz de incógnitas, donde cada término se corresponde con una de las
representa al coeficiente que acompaña a la j-ésima incógnita de la ecuación i-ésima. La segunda es la matriz de incógnitas, donde cada término se corresponde con una de las  incógnitas que queremos averiguar. Y la tercera matriz es la de términos independientes, donde el cada
incógnitas que queremos averiguar. Y la tercera matriz es la de términos independientes, donde el cada 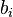 representa al término independiente de la ecuación i-ésima.
representa al término independiente de la ecuación i-ésima.Esta representación matricial facilita el uso de algunos métodos de resolución, como el método de Gauss, en el que, partiendo de la matriz aumentada (matriz de coeficientes a la que se le ha acoplado la matriz de términos independientes), y aplicando transformaciones lineales sobre las ecuaciones, pretendemos llegar a una matriz de este tipo:
Una vez la matriz se ha triangulado, el valor de cada término
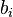 se corresponderá con el de la incógnita
se corresponderá con el de la incógnita 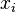 . Si nos encontramos alguna fila del tipo
. Si nos encontramos alguna fila del tipo  , con
, con  , el sistema no tendrá solución.
, el sistema no tendrá solución.Tipos de soluciones.
Existencia de soluciones.
El teorema de la función inversa proporciona condiciones suficientes de existencia de solución, de un sistema como con . Si sucede que la función vectorial:
. Si sucede que la función vectorial:Es diferenciable con continuidad, es decir, es de clase
 y su jacobiano no se anula en ningún punto entonces existe una única solución del sistema. Ya que en ese caso existirá una función inversa, y podremos escribir la solución buscada simplemente como:
y su jacobiano no se anula en ningún punto entonces existe una única solución del sistema. Ya que en ese caso existirá una función inversa, y podremos escribir la solución buscada simplemente como:Sin embargo, la condición de diferenciabilidad anterior aún siendo condición suficiente, no es una condición necesaria, por lo que existen sistemas de ecuaciones en que las funciones
 no son diferenciables y sin embargo, existen soluciones. Más aún, en casos en que existe más de una solución si la función es diferenciable entonces el jacobiano se anula en algún punto, pero eso no impide que existan varias soluciones.
no son diferenciables y sin embargo, existen soluciones. Más aún, en casos en que existe más de una solución si la función es diferenciable entonces el jacobiano se anula en algún punto, pero eso no impide que existan varias soluciones.En casos de un menor número de ecuaciones que de incógnitas, cuando
 , entonces el sistema es compatible indeterminado o carece de soluciones. En esos casos, el teorema de la función implícita proporciona condiciones suficientes, aunque no necesarias, para la existencia de soluciones de un modo similar a como el teorema de la función inversa las proporciona en el caso
, entonces el sistema es compatible indeterminado o carece de soluciones. En esos casos, el teorema de la función implícita proporciona condiciones suficientes, aunque no necesarias, para la existencia de soluciones de un modo similar a como el teorema de la función inversa las proporciona en el caso  .
.Métodos de resolución.
Si bien para los sistemas de ecuaciones lineales existen multitud de técnicas del álgebra lineal, para los sistemas de ecuaciones no-lineales el problema es técnicamente bastante más difícil.Métodos analíticos.
Los métodos analíticos se restringen casi exclusivamente a sistemas de ecuaciones lineales. Ni siquiera se conoce una solución analítica para el sistema de ecuaciones de segundo grado general:Métodos numéricos
Las aplicaciones técnicas generalmente recurren a algoritmos numéricos que permiten calcular aproximaciones numéricas a las solciones de un sistema de ecuaciones.Uno de los métodos numéricos que puede generalizarse a sistemas no-lineales es el método de Newton-Raphson. En el caso multidimensional la resolución numérica del sistema de n ecuaciones
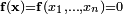 puede hacerse a partir del conocimiento de una solución aproximada
puede hacerse a partir del conocimiento de una solución aproximada  , siempre y cuando la aplicación anterior sea difernciable, mediante el esquema iterativo:
, siempre y cuando la aplicación anterior sea difernciable, mediante el esquema iterativo:O más explícitamente:
Lamentablemente la convergencia del esquema iterativo anterior no está garantizada y en casos de soluciones múltiples la convergencia puede darse hacia la solución no deseada.
Métodos gráficos
Los métodos gráficos son didácticos e elustrativos, aunque en general carecen de interés práctico en las aplicaciones técnicas de importancia. Además están restringidos generalmente a sistemas de dos o tres ecuaciones reales.Dos sistemas de ecuaciones con dos incognitas de valor real, suelen aparecer como uno de los cinco tipos diferentes mencionados a continuación. Tienen una relación con el número de soluciones:
- Aquellos sitemas de ecuaciones que representan gráficamente rectas y curvas que se intersectan entre si. Este tipo de sistema de ecuación es considerado como el normal. Suele tener un numero de soluciones finito cada uno formado por las coordenadas de los punto de intersección.
- Sistemas que tienen simplificaciones falsas. Por ejemplo: 1 = 0. Graficamente se representan como un conjunto de lineas que nunca se intersectan entre si, como lineas paralelas.
- Sistemas de ecuaciones en las que ambos simplificar a una identidad (por ejemplo, x = 2x - y 0 y x = 0). Cualquier asignación de valores a las variables desconocidas satisface las ecuaciones. Por lo tanto, hay un número infinito de soluciones, que gráficamente, se representa como todos los puntos del plano que representa la solución.
- Sistemas en los que las dos ecuaciones representan el mismo conjunto de puntos: son matemáticamente equivalentes (una ecuación general puede ser transformada en otra a través de la manipulación algebraica). Estos sistemas representan completamente la superposición de líneas o curvas, etc Una de las dos ecuaciones es redundante y puede ser desechada. Cada punto de la serie de puntos corresponde a una solución. Generalmente, esto significa que hay un número infinito de soluciones.
- Sistemas en los que una (y sólo una) de las dos ecuaciones se simplifica a una identidad. Por lo tanto, es redundante y puede ser descartada, según el tipo anterior. Cada punto de la serie de puntos representados por los demás es una solución de la ecuación de los que hay a continuación, por lo general un número infinito.
Interpretacion Geometrica.
Resolución y representación gráfica de sistemas de ecuaciones lineales
Resolvemos gráficamente el sistema x + y = 6; x - y = 2}
- o Despejamos y en las dos ecuaciones. x + y = 6 → y = 6 - x
x - y = 2 → y = x - 2
- o Dando valores a x, formamos una tabla de valores para cada una de las dos ecuaciones.
y = 6 - x
| x | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| y | 6 | 5 | 4 | 3 | 2 |
| x | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| y | -2 | -1 | 0 | 1 | 2 |
- o Representamos estos puntos sobre un sistema de ejes.
 Uniendo los puntos de cada ecuación, obtenemos dos rectas que representan todas las soluciones de cada una de las ecuaciones
Uniendo los puntos de cada ecuación, obtenemos dos rectas que representan todas las soluciones de cada una de las ecuaciones - o Puede ocurrir uno de los siguientes casos:
- Si las rectas no se cortan, es decir, son paralelas, el sistema es incompatible, no tiene solución.
- Si las rectas se cortan en un punto, el sistema tiene solución única. Decimos que es compatible determinado.
- Si las dos rectas coinciden, esto es, son la misma, el sistema tiene infinitas soluciones. Es un sistema compatible indeterminado.
Clasificamos los siguientes sistemas de ecuaciones lineales
- a) b) c)
- a) Dibujamos las rectas que representan las soluciones de cada ecuación: Dos soluciones de la primera ecuación son: x = 1, y = 4; x = 2, y = 2
Dos soluciones de la segunda ecuación son:
x = 1, y= 0; x = 2, y = 2
Las rectas se cortan en un punto que será la solución:x = 2, y = 2. Por tanto, el sistema será compatible determinado. Vemos la representación en el margen.
b) Dibujamos las rectas que representan las soluciones de cada ecuación: Dos soluciones de la primera ecuación son:
x = 0, y = 3; x = 3, y = 0
Dos soluciones de la segunda ecuación son:
x = 1, y = 2; x = 2, y = 1
Las rectas coinciden, toda la recta es solución del sistema (infinitas soluciones). Por tanto, el sistema será compatible indeterminado. Vemos la representación en el margen.
c) Dibujamos las rectas que representan las soluciones de cada ecuación: Dos soluciones de la primera ecuación son:
x = 0,y = 3; x = 3,y = 0
Dos soluciones de la segunda ecuación son:
x = 0, y =-1; x = -2, y = 1
Las rectas son paralelas, no tienen ningún punto en común, luego el sistema no tiene solución. Por tanto, el sistema será incompatible. Vemos la representación siguiente:
 Representación gráfica de los tres sistemas
Representación gráfica de los tres sistemas Metodos de solucion de sistemas de ecuaciones lineales.
Sustitución.
El metodo de sustitución consiste en despejar en una de las ecuaciones cualquier incógnita, preferiblemente la que tenga menor coeficiente, para, a continuación, sustituirla en otra ecuación por su valor.En caso de sistemas con más de dos incógnitas, la seleccionada debe ser sustituida por su valor equivalente en todas las ecuaciones excepto en la que la hemos despejado. En ese instante, tendremos un sistema con una ecuación y una incógnita menos que el inicial, en el que podemos seguir aplicando este método reiteradamente. Por ejemplo, supongamos que queremos resolver por sustitución este sistema:
En la primera ecuación, seleccionamos la incógnita
 por ser la de menor coeficiente y que posiblemente nos facilite más las operaciones, y la despejamos, obteniendo la siguiente ecuación.
por ser la de menor coeficiente y que posiblemente nos facilite más las operaciones, y la despejamos, obteniendo la siguiente ecuación.El siguiente paso será sustituir cada ocurrencia de la incógnita
 en la otra ecuación, para así obtener una ecuación donde la única incógnita sea la
en la otra ecuación, para así obtener una ecuación donde la única incógnita sea la  .
.Al resolver la ecuación obtenemos el resultado
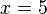 , y si ahora sustituimos esta incógnita por su valor en alguna de las ecuaciones originales obtendremos
, y si ahora sustituimos esta incógnita por su valor en alguna de las ecuaciones originales obtendremos  , con lo que el sistema queda ya resuelto.
, con lo que el sistema queda ya resuelto.Igualación.
El método de igualación se puede entender como un caso particular del método de sustitución en el que se despeja la misma incógnita en dos ecuaciones y a continuación se igualan entre sí la parte derecha de ambas ecuaciones.Tomando el mismo sistema utilizado como ejemplo para el método de sustitución, si despejamos la incógnita
 en ambas ecuaciones nos queda de la siguiente manera:
en ambas ecuaciones nos queda de la siguiente manera:Como se puede observar, ambas ecuaciones comparten la misma parte izquierda, por lo que podemos afirmar que las partes derechas también son iguales entre sí.
Llegados a este punto, la ecuación resultante es resoluble y podemos obtener el valor de la incógnita
 , y a partir de aquí, sustituyendo dicho valor en una de las ecuaciones originales, obtener el valor de la
, y a partir de aquí, sustituyendo dicho valor en una de las ecuaciones originales, obtener el valor de la  , que además ya se encuentra despejada.
, que además ya se encuentra despejada.La forma más fácil de tener el método de sustitución es realizando un cambio para despejar x después de averiguar el valor de la y.
Reducción.
Este método suele emplearse mayoritariamente en los sistemas lineales, siendo pocos los casos en que se utiliza para resolver sistemas no lineales. El procedimiento, diseñado para sistemas con dos ecuaciones e incógnitas, consiste en transformar una de las ecuaciones (generalmente, mediante productos), de manera que obtengamos dos ecuaciones en la que una misma incógnita aparezca con el mismo coeficiente y distinto signo. A continuación, se suman ambas ecuaciones produciéndose así la reducción o cancelación de dicha incógnita, obteniendo así una ecuación con una sola incógnita, donde el método de resolución es simple.Por ejemplo, en el sistema:
no tenemos más que multiplicar la primera ecuación por
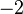 para poder cancelar la incógnita
para poder cancelar la incógnita  . Al multiplicar, dicha ecuación nos queda así:
. Al multiplicar, dicha ecuación nos queda así: ha sido reducida y que, en este caso, nos da directamente el valor de la incógnita
ha sido reducida y que, en este caso, nos da directamente el valor de la incógnita  :
: en cualquiera de las ecuaciones donde aparecían ambas incógnitas, y obtener así que el valor de
en cualquiera de las ecuaciones donde aparecían ambas incógnitas, y obtener así que el valor de  es igual a
es igual a  .
.Método de Gauss.
La eliminación de Gauss-Jordan, más conocida como método de Gauss, es un método aplicable únicamente a los sistemas lineales de ecuaciones, y consistente en triangular la matriz aumentada del sistema mediante transformaciones elementales, hasta obtener ecuaciones de una sola incógnita, cuyo valor será igual al coeficiente situado en la misma fila de la matriz. Este procedimiento es similar al anterior de reducción, pero ejecutado de manera reiterada y siguiendo un cierto orden algorítmico.
Tomemos como ejemplo el siguiente sistema:Su matriz aumentada será esta:
En primer lugar, reducimos la incógnita
 , sumando a la segunda fila, la primera multiplicada por
, sumando a la segunda fila, la primera multiplicada por  , y a la tercera, la primera fila. La matriz queda así:
, y a la tercera, la primera fila. La matriz queda así:El siguiente paso consiste en eliminar la incógnita
 en la primera y tercera fila, para lo cual les sumamos la segunda multiplicada por
en la primera y tercera fila, para lo cual les sumamos la segunda multiplicada por 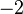 y por
y por  , respectivamente.
, respectivamente.Por último, eliminamos la
 , tanto de la primera como de la segunda fila, sumándoles la tercera multiplicada por
, tanto de la primera como de la segunda fila, sumándoles la tercera multiplicada por 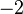 y por
y por  , respectivamente:
, respectivamente:Llegados a este punto podemos resolver directamente las ecuaciones que se nos plantean:
O, si lo preferimos, podemos multiplicar las tres filas de la matriz por:
 ,
, 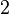 y
y  respectivamente, y obtener así automáticamente los valores de las incógnitas en la última columna.
respectivamente, y obtener así automáticamente los valores de las incógnitas en la última columna.Regla de Cramer.
La regla de Cramer da una solución para sistemas compatibles determinados en términos de determinantes y adjuntos dada por:Donde Aj es la matriz resultante de remplazar la j-ésima columna de A por el vector columna b. Para un sistema de dos ecuaciones y dos incónitas:
La regla de Cramer da la siguiente solución:
Nota: Cuando en la determinante original det(A) el resultado es 0, el sistema indica múltiples o sin coincidencia.
Sistemas lineales en un cuerpo arbitrario.
Cuando consideramos ecuaciones lineales cuyas soluciones son números racionales, reales o complejos o más generalmente un cuerpo , la solución puede encontrarse mediante Regla de Cramer. Para sistemas de muchas ecuaciones la regla de Cramer puede ser computacionalmente más costosa y suelen usarse otros métodos más "económicos" en número de operaciones como la eliminación de Gauss-Jordan y la descomposición de Cholesky. Existen también métodos indirectos (basados en iteraciones) como el método de Gauss-Seidel.
, la solución puede encontrarse mediante Regla de Cramer. Para sistemas de muchas ecuaciones la regla de Cramer puede ser computacionalmente más costosa y suelen usarse otros métodos más "económicos" en número de operaciones como la eliminación de Gauss-Jordan y la descomposición de Cholesky. Existen también métodos indirectos (basados en iteraciones) como el método de Gauss-Seidel.Si el cuerpo es infinito (como es el caso de los números reales o complejos), entonces solo puede darse una de las tres siguientes situaciones:
- el sistema no tiene solución (en dicho caso decimos que el sistema está sobredeterminado o que es incompatible)
- el sistema tiene una única solución (el sistema es compatible determinado)
- el sistema tiene un número infinito de soluciones (el sistema es compatible indeterminado).
- Ax = 0
Se han diseñado algoritmos alternativos mucho más eficientes a la eliminación de Gauss-Jordan para una gran cantidad de casos específicos. La mayoría de estos algoritmos mejorados tienen una complejidad computacional de O(n²). Algunos de los métodos más usados son:
- Para los problemas de la forma Ax = b, donde A es una matriz de Toeplitz simétrica, se puede utilizar la recursión de Levinson o alguno de los métodos derivados de éste. Un método derivado de la recursión de Levinson es la recursión de Schur, que es ampliamente usado en el campo del procesamiento digital de señales.
- Para los problemas de la forma Ax = b, donde A es una matriz singular o casi singular, la matriz A se descompone en el producto de tres matrices en un proceso llamado descomposición de valores singulares.
Solución de sistemas lineales en un anillo.
Los métodos para resolver el sistema sobre un anillo son muy diferentes a los considerados anteriormente. De hecho la mayoría de métodos usados en cuerpos, como la regla de Cramer, son inaplicables en anillos debido a que no existen inversos multiplicativos.La existencia de solución del sistema sobre los enteros requiere varias condiciones:
- Para cada i
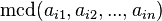 es divisor de
es divisor de  .
. - Si la condición anterior se cumple para un determinado i existe un conjunto de enteros
 formado por el conjunto de enteros que satisface la i-ésima ecuación, y existirá solución si la intersección
formado por el conjunto de enteros que satisface la i-ésima ecuación, y existirá solución si la intersección  .
.
http://es.wikipedia.org/wiki/Sistema_de_ecuaciones
http://mx.kalipedia.com/matematicas-algebra/tema/resolucion-representacion-grafica-sistemas.html?x1=20070926klpmatalg_145.Kes&x=20070926klpmatalg_146.Kes
http://es.wikipedia.org/wiki/Sistema_de_ecuaciones_lineales
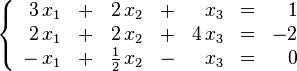





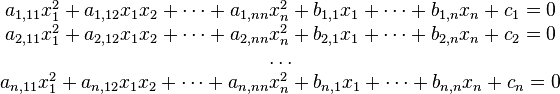
![\mathbf{x}^{(m+1)} = \mathbf{x}^{(m)} - [D\mathbf{f}(\mathbf{x}^{(m)})]^{-1}(\mathbf{f}(\mathbf{x}^{(m))}), \qquad \mathbf{f}:\R^n \to \R^n,\ \mathbf{f}\in C^{(1)}(\R^n;\R^n)](http://upload.wikimedia.org/math/4/7/b/47b55c8103dcddc4a726197d531130a5.png)




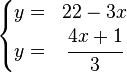







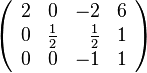








No hay comentarios:
Publicar un comentario